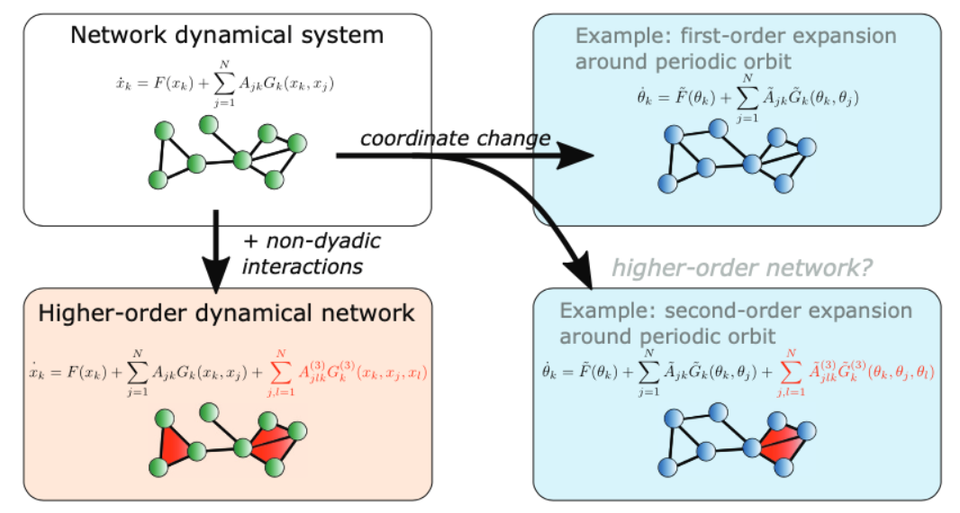
What are higher-order networks?

Networks - as mathematical representations of interconnected units - 
are relevant in a wide range of real-wold systems, ranging from 
interconnected neural cells in the brain to relationship networks 
between authors of scientific articles. Traditionally, networks have 
been equated with the mathematical concept of a graph that specifies 
relations between pairs of individual units. While this approach has 
produced for example powerful tools to analyze data, there has been a 
shift to recognize the importance of relations and interactions beyond 
pairs, namely relations between more than two individual units.

In the paper What are higher-order networks? published recently in 
SIAM Review, VU mathematician C Bick and 
coauthors take account of these recent developments from a mathematical 
perspective. They provide a unified perspective on recent research where 
nonpairwise interactions play a role. These range from topological data 
analysis to network dynamical systems, thereby connecting different 
research directions of interest to the Department of Mathematics at the VU.