1 min read Papers

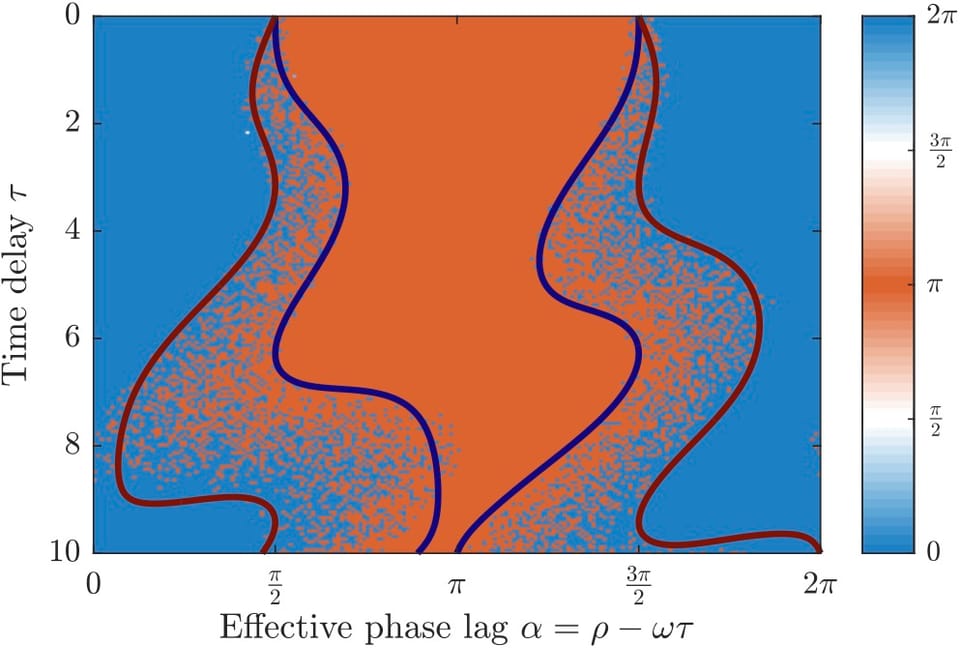
Preprint on high-order phase reductions for delay-coupled networks

Preprint on high-order phase reductions for delay-coupled networks
Second order phase reduction of two delay-coupled Stuart—Landau oscillators predicts synchronisation behaviour (blue and red curve) in agreement with numerical simulation (blue and orange shading)

Coupled oscillators with time-delayed network interactions are critical to understand synchronization phenomena in many physical systems. Phase reductions to finite-dimensional phase oscillator networks allow for their explicit analysis, including an analysis of synchronization behavior. 

A new preprint, resulting from a collaboration by VU mathematicians C. Bick, B. Rink and B. de Wolff, develops a general and systematic approach to compute phase reductions for oscillator networks with time-delayed interactions, up to arbitrary order in the coupling strength. Through an explicit example, we show how this approach provides a new way to understand delay-induced synchronization phenomena.