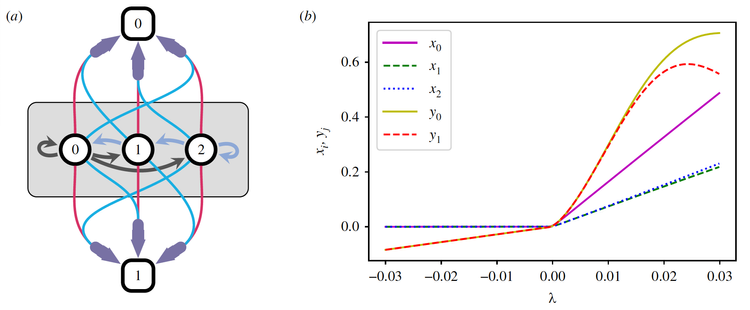
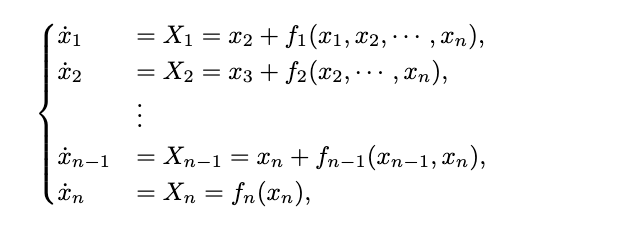Reluctant bifurcations organize synchrony breaking in hypernetworks
A new paper of Eddie Nijholt (Imperial College), Bob Rink (VU) and Sören von de Gracht (Paderborn) was published today
New preprint proves existence of quasi-patterns in spatially extended PDEs
Quasi-patterns are symmetric solutions of spatially extended PDEs which are non-periodic but have a discrete diffraction diagram. Such patterns have
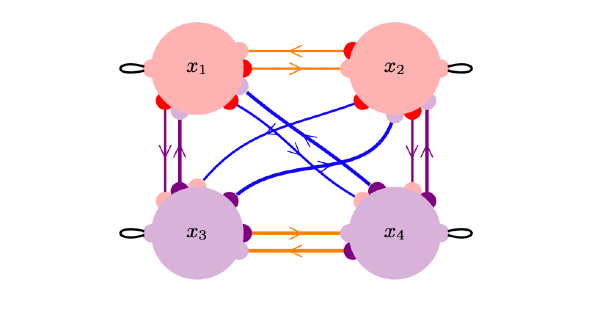
The Lie algebraic structure of colored networks
Fahimeh Mokhtari and Jan Sanders from the Mathematics Department of Vrije Universiteit Amsterdam explore the structural properties of colored network
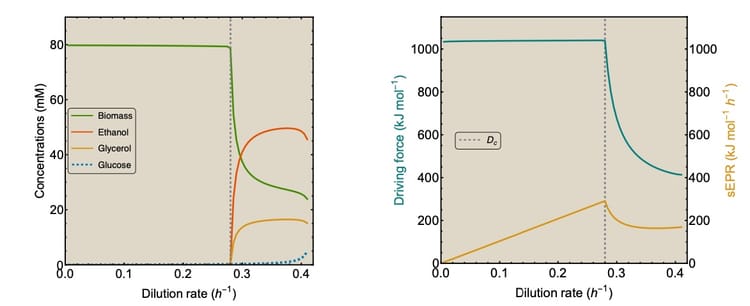
New preprint on the relation between entropy production rate and microbial growth rate
Entropy production rate is a measure for energy dissipation rate in the cell and quantifies irreversibility. In this preprint, the
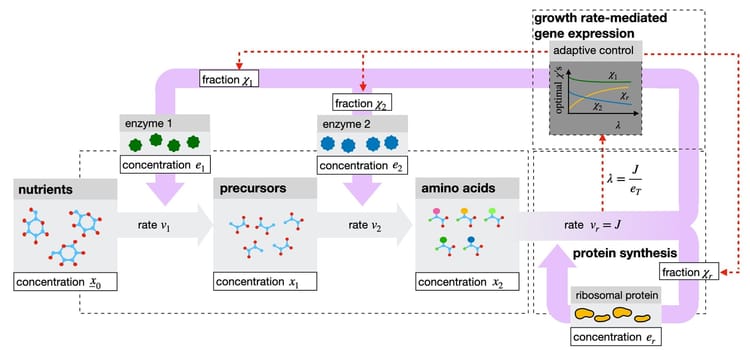
New preprint on robust adaptation by single-celled organisms to environmental changes
Single-celled organisms such as bacteria are able to tune enzyme levels that catalyze the reaction pathways by which they eventually
Paper on well-posedness of neural fields with anisotropic diffusion
A new paper by Amsterdam Dynamics member Daniele Avitabile, and collaborators Nikolai Chemetov and Pedro Lima studies well-posedness of solutions
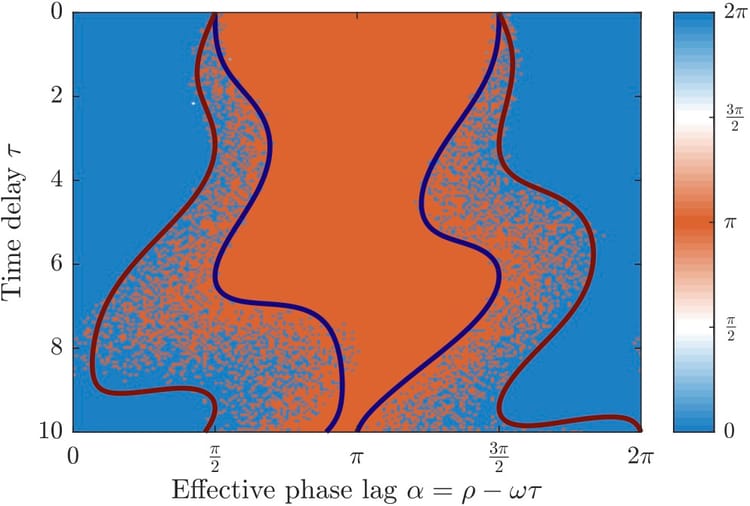
Preprint on high-order phase reductions for delay-coupled networks
Coupled oscillators with time-delayed network interactions are critical to understand synchronization phenomena in many physical systems. Phase reductions to finite-dimensional
What are higher-order networks?
Networks - as mathematical representations of interconnected units -
are relevant in a wide range of real-wold systems, ranging from
Calculating infinity minus infinity
Establishing stability and instability of stationary states is a basic
requirement for understanding dynamics. Counting the dimension of the unstable